 |
Численными методы решения уравнений.
Введение. Существуют задачи, которые не решаются аналитически или требуют больших временных затрат. Для решения данного типа задач используют численные методы – методы, позволяющие получить приближенное решение поставленной задачи с заданной степенью точности. При решении задач численными методами в настоящее время часто используется ЭВМ. Этапы решения задачи с использованием ЭВМ:
Построение математической модели – наиболее важный этап. Если модель очень грубо отражает исследуемый объект, то даже самые точные вычисления не смогут дать удовлетворительных результатов. Математическая модель может иметь вид уравнения, системы уравнений или быть выражена в форме иных математических структур или соотношений. 1. Погрешности численного решения задач. В отличие от аналитического решения, численное решение задачи всегда сопровождается накоплением погрешностей. Источники погрешностей:
Виды погрешностей:
Результирующая погрешность определяется как сумма величин всех видов погрешностей. Определение погрешностей Любое определение величины (измерение или расчет) считается завершенным только тогда, когда определен интервал допустимых отклонений от истинного значения измеряемой величины. Абсолютная и относительная погрешности. Если x – точное значение величины и xi – известное приближение к нему, то абсолютной погрешностью приближенного значения xi называют величину Δxi, про которую известно, что |xi-x|≤Δxi
Результат вычислений следует записывать или Пример. Были трижды произведены измерения некоторой величины. Результаты измерений сведены в таблицу.
В данном примере за истинное значение величины следует принять среднее арифметическое Δaср – средняя абсолютная погрешность, ε = Δaср/aср – относительная погрешность. Результатом измерений будет a = 12.3 ± 0.1; ε = 0.8% Примечание: число значащих цифр в записи величины и ее погрешности должно быть одинаковым! Вычислительная погрешность. Погрешность суммирования/вычитания z = x ± y: абсолютная погрешность Δz = Δx + Δy относительная погрешность εz = Погрешность умножения z = x*y абсолютная погрешность Δz = x*Δy + y*Δx относительная погрешность εz = εx + εy Погрешность деления z = x/y абсолютная погрешность Δz = относительная погрешность εz = εx + εy Пример. Определить силу тока в цепи, если номинальное сопротивление резистора R = 6 Ом ± 2%, а вольтметр показывает напряжение U = 12 В, погрешность вольтметра составляет 0.1 В. По закону Ома для участка цепи сила тока определяется как I = U/R, следовательно: I = 12 В / 6 Ом = 2 А Для определения абсолютной и относительной погрешностей величины силы тока нужно знать соответствующие погрешности для напряжения и сопротивления. ΔU = 0.1 В, εU = ΔU/U = 0.1 В/ 12 В = 0.01 εR = 2% = 0.02, ΔR = εR * R = 0.02 * 6 Ом = 0.12 Ом εI = εI = εU + εR = 0.01 + 0.02 = 0.03 Таким образом I = 2.00 A ± 0.03 A; ε = 0.03 2. Решение уравнений с одной переменной. В общем случае уравнение можно представить в виде: F(x) = 0, где функция F(x) определена и непрерывна на конечном или бесконечном интервале [a, b]. Всякое число k �AA [a, b], обращающее функцию F(x) в нуль, т.е. такое, при котором F(k) = 0, называется корнем уравнения. Нелинейные уравнения с одной неизвестной подразделяются на алгебраические и трансцендентные. Уравнение называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из каждого алгебраического уравнения можно получить уравнение в каноническом виде:
где a0, a1, … an, - коэффициенты уравнения, x – неизвестное. Уравнение называется трансцендентным, если функция не является алгебраической, например:
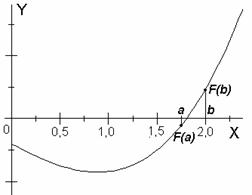
Решить уравнение означает: - установить, имеет ли оно корни; - определить число корней уравнения; - найти значения коней уравнения с заданной точностью. Наиболее распространенными на практике численными методами решения уравнения с одной неизвестной являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации и некоторые другие. 2.1. Отделение корней. Отделение корней – процедура нахождения отрезков, на которых уравнение F(x) имеет только один корень. В большинстве случаев отделение корней можно провести графически, для этого достаточно построить график функции F(x) и определить отрезки, на которых эта функция имеет только одну току пересечения с осью абсцисс. В случаях, когда построение графика затруднительно, отделение корней следует подкреплять вычислениями. Если непрерывная функция принимает на концах отрезка [a, b] значения разных знаков (т.е. F(a)*F(b)<0), то уравнение F(x) имеет на этом отрезке, по меньшей мере, один корень. Если функция F(x) при этом строго монотонна, то корень на отрезке единственный. Так, например, для функции, заданной на отрезке [0, 2] (рис. 1) существует единственный корень, который следует уточнять на отрезке [1.75, 2].
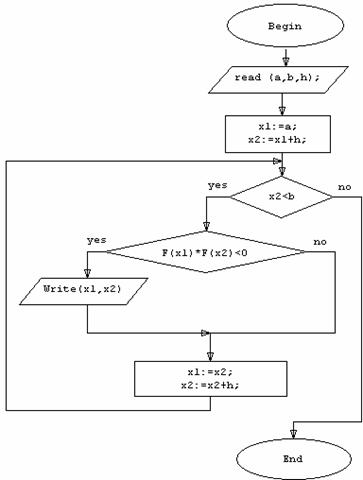
Рис. 1. Графическое отделение корней. Для отделения корней удобно использовать ЭВМ. Допустим, что корни уравнения F(x) лежат на отрезке [A, B]. Требуется отделить корни уравнения, т.е. указать все отрезки [a, b] ∋ [A, B], содержащие по одному корню. Вычислим значения F(x) с некоторым шагом h начиная с точки a. Как только обнаружится пара соседних значений F(x), имеющих разные знаки, так соответствующие значения аргумента x можно считать концами отрезка, содержащего корень. Блок-схема алгоритма отделения корней приведена на рис. 2.
Рис. 2. Блок-схема процедуры отделения корней.
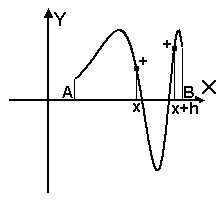
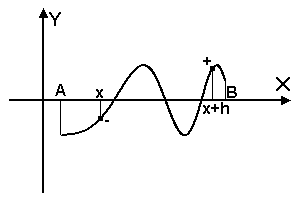
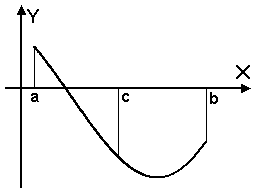
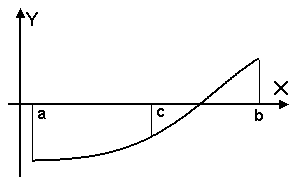
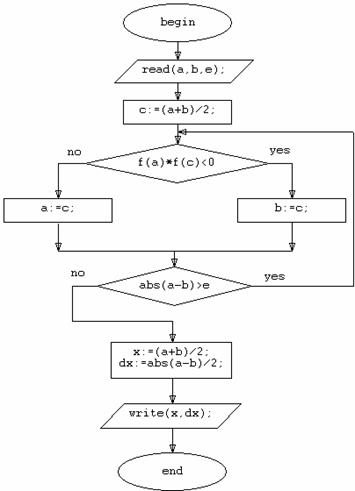
а) б) Рис. 3. При отделении корней следует учитывать, что если функция немонотонна на отрезке [x, x+h], то существует возможность либо пропустить корень (рис.3а), либо отделить отрезок более чем с одним корнем (рис.3б). 2.2. Метод половинного деления. Метод половинного деления один из наиболее простых методов поиска корней функции, к тому же обладающий гарантированной сходимостью при условии, что корни отделены правильно. Пусть функция F(x) на отрезке [a, b] непрерывна и имеет единственный корень. Разделим отрезок [a, b] пополам точкой c = (a + b)/2. Если F(c) ≠ 0, то возможны два случая: либо функция меняет знак на отрезке [a, c] (рис. 4а), либо на отрезке [c, b] (рис. 4б). Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.
а) б) Рис. 4. Вычисления следует остановить, если выполняется одно из следующих условий: |F(c)|<ε или β – α < ε, где α и β - полученные границы отрезка, а ε – заданная точность вычислений. Корнем уравнения, полученным данным методом можно приближенно считать число x = (α + β)/2. Погрешность метода определяется как Δx = (β – α)/2. Блок-схема алгоритма метода половинного деления приведена на рис. 5.
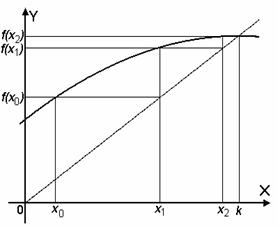
Рис. 5. Блок-схема метода половинного деления. 2.3. Метод простой итерации. Уравнение F(x) = 0 можно заменить равносильным ему уравнением x = f(x). (*) Пусть k – корень уравнения (*), а x0 – полученное каким-либо способом нулевое приближение к корню k. Подставляя x0 в правую часть уравнения (*), получим некоторое значение x1 = f(x0). Проделаем то же самое x1, получим x2 = f(x1) и т.д. Повторение описанной процедуры, где xn = f(xn-1) позволяет получить числовую последовательность: x0, x1, …, xn, …, (**) которую называют последовательностью приближений или итерационной последовательностью (от лат. iteratio – повторение). Процесс построения итерационной последовательности имеет наглядную геометрическую интерпретацию (рис. 6).
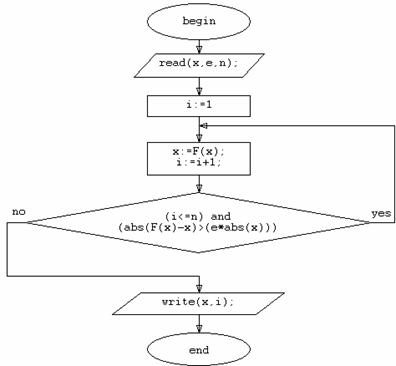
Рис.6. Геометрическая интерпретация метода простой итерации Последовательность приближений может быть сходящейся или расходящейся. На рис. 6 приведен пример сходящейся последовательности. Если итерационная последовательность (**) сходится и функция f(x) непрерывна, то предел последовательности (**) является корнем уравнения (*). То есть при n→∞, xn→ f(xn). Итерационная последовательность f(xn-1) (n = 1, 2…) сходится при любом начальном x0 ∈ [a, b] если выполняются следующие условия: 1) f(x) определена и дифференцируема на отрезке [a, b]; 2) f(x) ∈ [a, b] для всех x ∈ [a, b]; 3) существует такое вещественное q, что На практике удобно пользоваться соотношением: если в точке пресечения графиков f(x) и y=x (численном нахождение производной функции рассматривается в последующих параграфах), то итерационная последовательность сходится. Блок-схема алгоритма нахождения корней уравнения методом простой итерации приведена на рис.7. в начале работы вводится начальное приближение x, относительная погрешность e и максимальное число итераций n. Процесс продолжается до тех пор, пока относительная точность для двух последовательных приближений не станет меньше e: |(xi+1 -xi )/xi |< e. Чтобы избежать зацикливания при расходящейся последовательности, функция прекращает работу после n итераций. Для контроля вычислений целесообразно выводить промежуточные значения x на печать.
Рис.7. Блок-схема метода простой итерации. |
Разное: |
||||||||||||||||||
Copyright © 2007 Владимир Середа |
||||||||||||||||||||
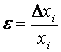, возможно выраженная в процентах.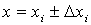
,
,
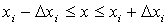
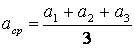
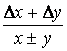
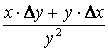
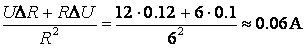
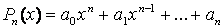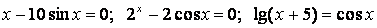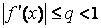для всех x ∈ [a, b];